Popular Sort Algorithms

Bài viết gồm 4 phần

Sort Algorithms Overview.

Simple sorts: Bubble sort, Insertion sort, and Selection sort.

Efficient sorts: Mergesort, Heapsort, Quicksort.

Distribution sort: Counting sort, Bucket sort, and Radix sort.

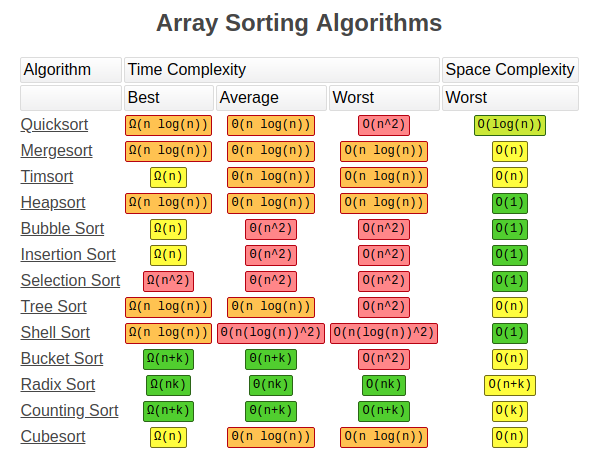
0. Sort Algorithms Overview - Theo VNOI

Ứng dụng về sắp xếp có ở khắp mọi nơi:

Một danh sách lớp với các học sinh được sắp xếp theo thứ tự bảng chữ cái.
Một danh bạ điện thoại.
Danh sách các truy vấn được tìm kiếm nhiều nhất trên Google.

Thuật toán sắp xếp cũng được dùng kết hợp với những thuật toán khác, như tìm kiếm nhị phân, thuật toán Kruskal để tìm cây khung nhỏ nhất của đồ thị.

Khi so sánh giữa các thuật toán này với nhau, có nhiều vấn đề phải quan tâm:

Thời gian chạy. Đối với các dữ liệu rất lớn, các thuật toán không hiệu quả sẽ chạy rất chậm và không thể ứng dụng trong thực tế.
Bộ nhớ. Các thuật toán nhanh đòi hỏi đệ quy sẽ có thể phải tạo ra các bản copy của dữ liệu đang xử lí. Với những hệ thống mà bộ nhớ có giới hạn (ví dụ embedded system), một vài thuật toán sẽ không thể chạy được.
Độ ổn định (stability). Độ ổn định được định nghĩa dựa trên điều gì sẽ xảy ra với các phần tử có giá trị giống nhau.
- Đối với thuật toán sắp xếp ổn định, các phần tử bằng với giá trị bằng nhau sẽ giữ nguyên thứ tự trong mảng trước khi sắp xếp.
- Đối với thuật toán sắp xếp không ổn định, các phần tử có giá trị bằng nhau sẽ có thể có thứ tự bất kỳ.

1. Simple sorts

1.1 Bubble sort - Theo VNOI

Đây là thuật toán cơ bản nhất cho việc sắp xếp. Ngoài ra, còn có tên khác là sinking sort.

Ý tưởng

Xét lần lượt các cặp 2 phần tử liên tiếp. Nếu phần tử đứng sau nhỏ hơn phần tử đứng trước, ta đổi chỗ 2 phần tử. Nói cách khác, phần tử nhỏ nhất sẽ nổi lên trên.
Lặp lại đến khi không còn 2 phần tử nào thỏa mãn. Có thể chứng minh được số lần lặp không quá N−1, do một phần tử chỉ có thể nổi lên trên không quá N−1 lần.

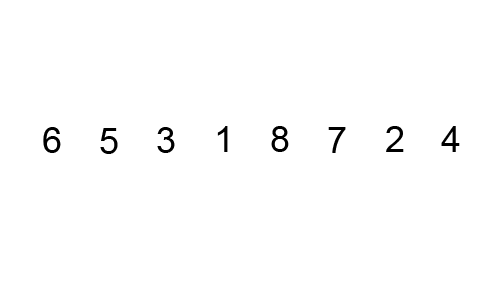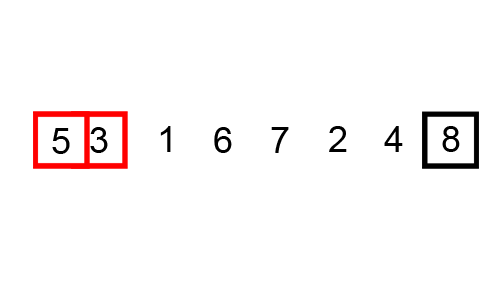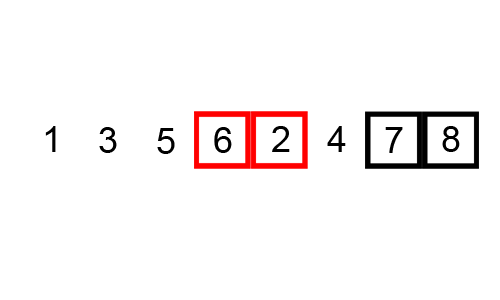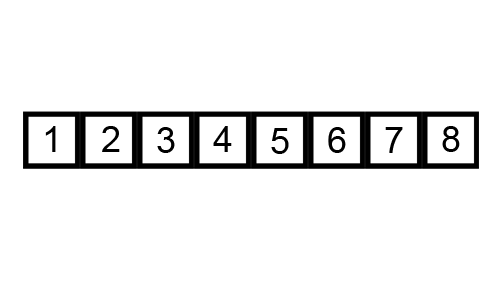
Source code minh hoạ

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n - 1; j++) {
        if (a[j] > a[j+1]) {
            swap(a[j], a[j+1]);
        }
    }
}

Độ phức tạp thuật toán

Time complexity: 0(n^2).
Space complexity: O(1).

Ưu điểm

Code đơn giản, dễ hiểu.
Không tốn thêm bộ nhớ.

Nhược điểm

Độ phức tạp O(n^2), không đủ nhanh với dữ liệu lớn.

Ứng dụng Không có.

1.2 Insertion sort

Là một thuật toán sắp xếp đơn giản, và không hiệu quả như các thuật toán sắp xếp nâng cao như quicksort, heapsort hay mergesort.

Ý tưởng: (sắp xếp tăng dần)

Duyệt từng phần tử i-th trong danh sách array ban đầu, và so sánh nó với từng phần tử k trong khoảng i-1 -> 0.
Nếu array[k] <= array[i], hoán đổi vị trí của array[k+1] với array[i].
Nếu array[k] > array[i], thì gán array[k+1] = array[k].

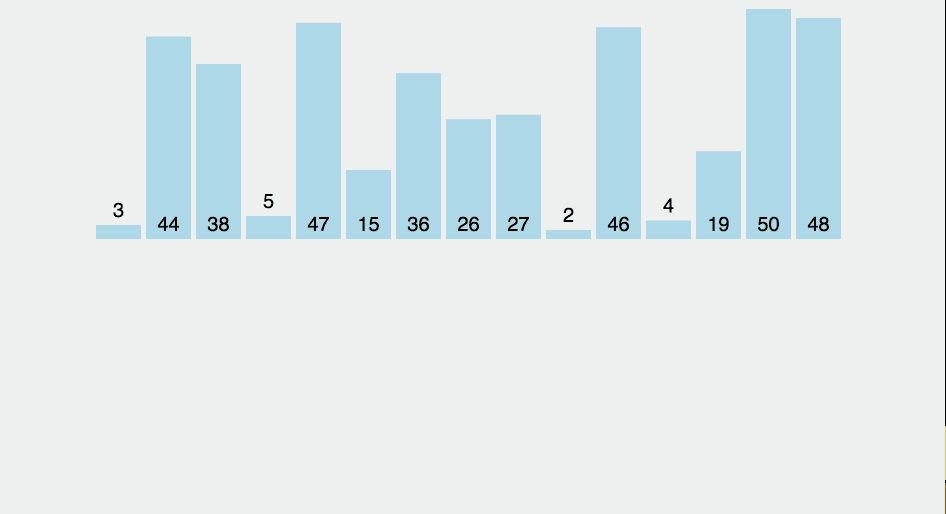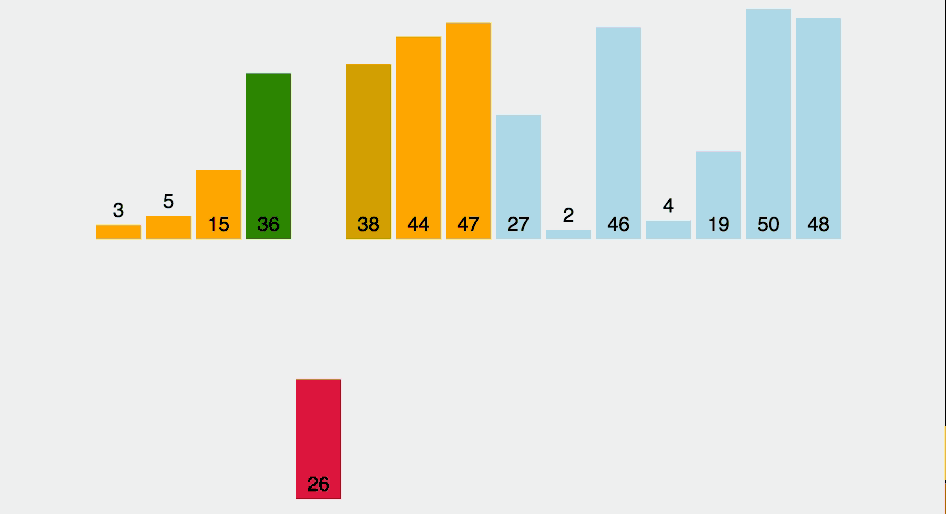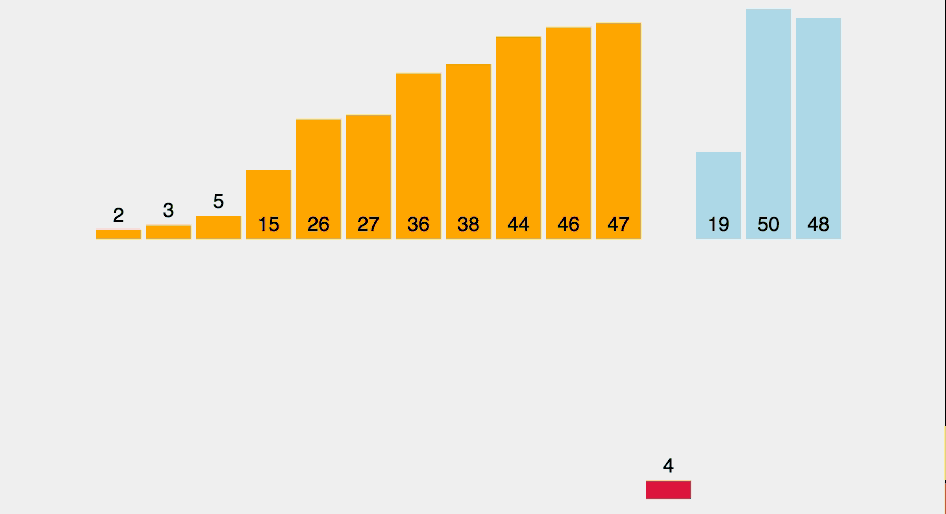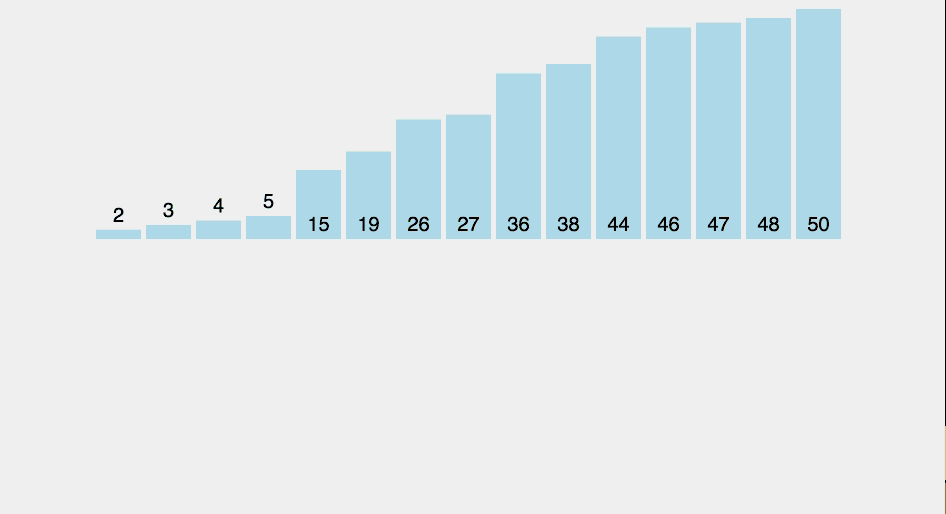
Source code minh hoạ

/*Function to sort array using insertion sort*/
void sort(int arr[]) 
{ 
    int n = arr.length; 
    for (int i = 1; i < n; ++i) { 
        int key = arr[i]; 
        int j = i - 1; 

        /* Move elements of arr[0..i-1], that are 
            greater than key, to one position ahead 
            of their current position */
        while (j >= 0 && arr[j] > key) { 
            arr[j + 1] = arr[j]; 
            j = j - 1; 
        } 
        arr[j + 1] = key; 
    } 
} 

Độ phức tạp thuật toán

Time complexity: O(n^2) với n là độ dài của array/list đầu vào.
Space complexity: O(1).

Ưu điểm

Cách cài đặt đơn giản.
Hiệu quả với những input có dữ liệu nhỏ và hiệu quả hơn những thuật toán sắp xếp có cùng độ phức tạp O(n^2) như selection sort hay bubble sort.
Ổn định: ví dụ, không thay đổi thứ tự tương quan của các phần tử có cùng key.
Sử dụng ít bộ nhớ (space complexity O(1))
Online: có thể sắp xếp dữ liệu từng phần dựa vào phần dữ liệu mà nó nhận được. Tham khảo online algorithm.

Nhược điểm

Độ phức tạp theo thời gian lớn O(n^2), không đủ nhanh với dữ liệu lớn.

Ứng dụng

Được sử dụng để sắp xếp các array/list mà có số lượng phần tử đủ nhỏ.
Được sử dụng để sắp xếp các phần tử mà gần như đã được sắp xếp trước đó. (khi đó, time complexity là O(n)).
Được sử dụng để sắp xếp các dãy con đủ nhỏ trong thuật toán sắp xếp quick-sort.
Trong C++, hàm sắp xếp mặc định std::sort sử dụng thuật toán sắp xếp là introsort (sử dụng ý tưởng chính là quicksort, nhưng khi size của array/list đủ nhỏ, để tăng performance, thì chuyển sang sử dụng insertion sort).

1.3 Selection sort

Tương tự như insertion sort, selection sort là một thuật toán sắp xếp đơn giản, và không hiệu quả như các thuật toán sắp xếp nâng cao như quicksort, heapsort hay mergesort.

Ý tưởng: (sắp xếp tăng dần)

Danh sách mảng kết quả ban đầu là rỗng.
Chia mảng ban đầu thành 2 phần: 1 mảng con đã được sắp xếp (tính từ phần tử 0-th → i-th) và 1 mảng con chưa được sắp xếp (tính từ phần tử i+1 th → max-i th).
Duyệt từng phần tử trong mảng con chưa được sắp xếp, tìm phần tử k-th có key là nhỏ nhất và hoán đổi vị trí của phần tử k-th với phần tử ngoài cùng bên trái của mảng con chưa được sắp xếp (trong trường hợp này là i+1 th).

Source code minh hoạ

void sort(int arr[]) 
{ 
    int n = arr.length; 
  
    // One by one move boundary of unsorted subarray 
    for (int i = 0; i < n-1; i++) 
    { 
        // Find the minimum element in unsorted array 
        int min_idx = i; 
        for (int j = i+1; j < n; j++) 
            if (arr[j] < arr[min_idx]) 
                min_idx = j; 
  
        // Swap the found minimum element with the first 
        // element 
        int temp = arr[min_idx]; 
        arr[min_idx] = arr[i]; 
        arr[i] = temp; 
    } 
} 

Độ phức tạp thuật toán

Time complexity: O(n^2) với n là độ dài của array/list đầu vào
Space complexity: O(1)

Ưu điểm

Cách cài đặt đơn giản.
Ổn định: ví dụ, không thay đổi thứ tự tương quan của các phần tử có cùng key.
Sử dụng ít bộ nhớ (space complexity O(1)).
Số lần hoán đổi vị trí giữa 2 phần tử trong mảng là thấp nhất (trường hợp xấu nhất là n-1).

Nhược điểm

Độ phức tạp theo thời gian lớn O(n^2), không đủ nhanh với dữ liệu lớn.

Ứng dụng

Được sử dụng để sắp xếp các array/list mà có số lượng phần tử đủ nhỏ.

2. Efficient sorts

2.1 Mergesort

Là một thuật toán sắp xếp hiệu quả và ổn định.

Ý tưởng Sắp xếp trộn hoạt động kiểu đệ quy:

Đầu tiên chia dữ liệu thành 2 phần, và sắp xếp từng phần, sau đó gộp 2 phần lại với nhau.
Để gộp 2 phần, ta làm như sau:
- Tạo một dãy A mới để chứa các phần tử đã sắp xếp.
- So sánh 2 phần tử đầu tiên của 2 phần. Phần tử nhỏ hơn ta cho vào A và xóa khỏi phần tương ứng.
- Tiếp tục như vậy đến khi ta cho hết các phần tử vào dãy A.

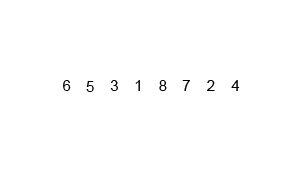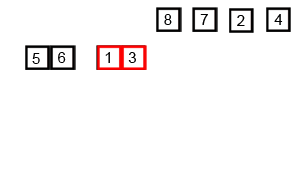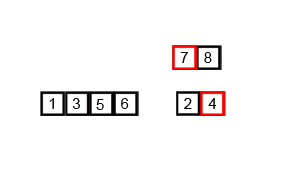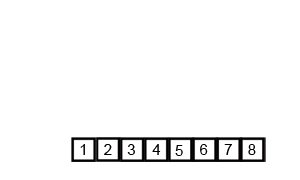
Source code minh hoạ

Có nhiều cách cài đặt mergesort, một trong số đó là cách tiếp cận top-down.

int a[MAXN]; // mảng trung gian cho việc sắp xếp

// Sắp xếp các phần tử có chỉ số từ left đến right của mảng data.
void mergeSort(int data[MAXN], int left, int right) {
    if (data.length == 1) {
        // Dãy chỉ gồm 1 phần tử, ta không cần sắp xếp.
        return ;
    }
    int mid = (left + right) / 2;
    // Sắp xếp 2 phần
    mergeSort(data, left, mid);
    mergeSort(data, mid+1, right);

    // Trộn 2 phần đã sắp xếp lại
    int i = left, j = mid + 1; // phần tử đang xét của mỗi nửa
    int cur = 0; // chỉ số trên mảng a

    while (i <= mid || j <= right) { // chừng nào còn 1 phần chưa hết phần tử.
        if (i > mid) {
            // bên trái không còn phần tử nào
            a[cur++] = data[j++];
        } else if (j > right) {
            // bên phải không còn phần tử nào
            a[cur++] = data[i++];
        } else if (data[i] < data[j]) {
            // phần tử bên trái nhỏ hơn
            a[cur++] = data[i++];
        } else {
            a[cur++] = data[j++];
        }
    }

    // copy mảng a về mảng data
    for (int i = 0; i < cur; i++) {
        data[left + i] = a[i];
    }
}

Độ phức tạp thuật toán

Time complexity: O(nlogn).
Space complexity: O(n).

Ưu điểm

Chạy nhanh, độ phức tạp O(nlogn).
Ổn định

Nhược điểm

Cần dùng thêm bộ nhớ để lưu mảng A.

Ứng dụng

phù hợp để sắp xếp danh sách liên kết
Perl 5.8 sử dụng merge sort như là thuật toán sắp xếp mặc định.
Trong Java, method Arrays.sort() sử dụng merge sort hay quicksort đã được cải tiến tuỳ thuộc vào loại dữ liệu, kết hợp với insertion sort để tăng performance.
Python và Java 7 sử dụng Timsort (cải tiến từ mergesort và insertion sort) là thuật toán sắp xếp mặc định.
Linux kernel sử dụng mergesort để sắp xếp danh sách liên kết.

2.2 Heapsort

Ý tưởng

Sử dụng cấu trúc dữ liệu heap để lưu trữ array/list đầu vào.
Ở mỗi bước, lấy ra phần tử nhỏ nhất trong heap, cho vào mảng đã sắp xếp.

Source code minh hoạ

Heap h = Heap();
for (int i = 0; i < n; i++) {
    // thêm phần tử vào heap
    h.push(data[i]);
}
int a[MAXN];
for (int i = 0; i < n; i++) {
    // lấy phần tử nhỏ nhất và cho vào mảng đã sắp xếp
    a[i] = h.pop();
}

Độ phức tạp thuật toán

Time complexity O(nlogn).
Space complexity O(1).

Ưu điểm

Cài đặt đơn giản nếu đã có sẵn thư viện Heap.
Chạy nhanh, độ phức tạp O(nlogn).

Nhược điểm

Không ổn định.

Ứng dụng

Heapsort thường được so sánh với quicksort:
- Quicksort nhanh hơn ở một số trường hợp, nhưng trường hợp xấu nhất, độ phức tạp thuật toán là O(n^2) ; trong khi heapsort luôn luôn có độ phức tạp là O(nlogn), nên ở những hệ thống nhúng mà liên quan tới real-time, hoặc hệ thống yêu cầu nhiều về bảo mật thì sẽ sử dụng heapsort, ví dụ như Linux kernel.
Heapsort cũng thường được so sánh với mergesort:
- Heapsort và mergesort có cùng time complexity, nhưng mergesort có space complexity là O(n), trong khi của heapsort chỉ là 0(1) , nên heapsort sẽ chạy nhanh hơn trên các thiết bị mà có data cache nhỏ hoặc chậm và không yêu cầu nhiều memory.
- Tuy nhiên, mergesort có nhiều ưu điểm so với heapsort:
  - mergesort trên array thì có performance tốt hơn so với heapsort, vì mergesort truy cập vào vùng nhớ liền nhau (contiguous memory locations), trong khi heapsort tham chiếu tới vùng nhớ heap.
  - Heapsort không ổn định; mergesort ổn định.
  - Mergesort có thể cài đặt để chạy song song (parallel implementation) để tăng performance, còn heapsort thì không.
  - Mergesort được áp dụng để thực hiện trên danh sách liên kết đơn với O(1) extra space, trong khi heapsort được áp dụng để thực hiện trên danh sách liên kết đôi với O(1) extra space.
  - Mergesort được sử dụng trong external sorting (để sắp xếp dữ liệu lớn), còn heapsort thì không.

Introsort là một thuật toán sắp xếp thay thế cho heapsort (kết hợp giữa heapsort và quicksort để tận dụng tối đa ưu điểm thời gian chạy trong trường hợp xấu nhất của heapsort và thời gian chạy trung bình của quicksort O(nlogn).

2.3 Quicksort - Theo VNOI

Ý tưởng

Chia dãy thành 2 phần, một phần “lớn” và một phần “nhỏ”.
- Chọn một khóa pivot
- Những phần tử lớn hơn pivot chia vào phần lớn.
- Những phần tử nhỏ hơn hoặc bằng pivot chia vào phần nhỏ.
Gọi đệ quy để sắp xếp 2 phần.

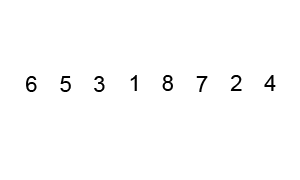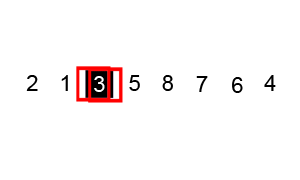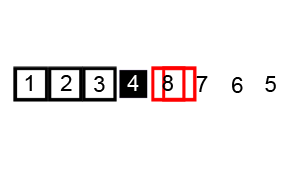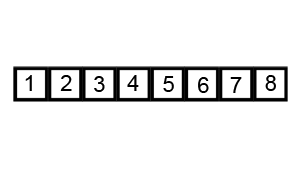
Source code minh hoạ

void quickSort(int a[], int left, int right) {
    int i = left, j = right;
    int pivot = a[left + rand() % (right - left)];
    // chia dãy thành 2 phần
    while (i <= j) {
        while (a[i] < pivot) ++i;
        while (a[j] > pivot) --j;

        if (i <= j) {
            swap(a[i], a[j]);
            ++i;
            --j;
        }
    }
    // Gọi đệ quy để sắp xếp các nửa
    if (left < j) quickSort(a, left, j);
    if (i < right) quickSort(a, i, right);
}

Độ phức tạp thuật toán

Time complexity: average O(nlogn), worst case O(n^2)
Space complexity: O(logn).

Ưu điểm

Chạy nhanh (nhanh nhất trong các thuật toán sắp xếp dựa trên việc só sánh các phần tử).

Nhược điểm

Tùy thuộc vào cách chia thành 2 phần, nếu chia không tốt, độ phức tạp trong trường hợp xấu nhất có thể là O(n^2). Nếu ta chọn pivot ngẫu nhiên, thuật toán chạy với độ phức tạp trung bình là O(nlogn) (trong trường hợp xấu nhất vẫn là O(n^2), nhưng ta sẽ không bao giờ gặp phải trường hợp đó).
Không ổn định.

Ứng dụng

Được sử dụng trong nhiều thư viện của các ngôn ngữ như Java, C++ (hàm sort của C++ dùng Introsort, là kết hợp của Quicksort và Insertion Sort).
Được sử dụng để sắp xếp array/list có size lớn.

3. Distribution sort

3.1 Counting sort

Counting sort là thuật toán sắp xếp hiệu quả, và là integer sorting với một array/list với các phần tử có key là integer không âm và đủ nhỏ.

Ý tưởng

Đếm số lượng các phần tử có key - value riêng biệt, và cập nhật vào một mảng trung gian với index chính là key value đó.
Từ mảng trung gian, xây dựng lại mảng kết quả ban đầu.

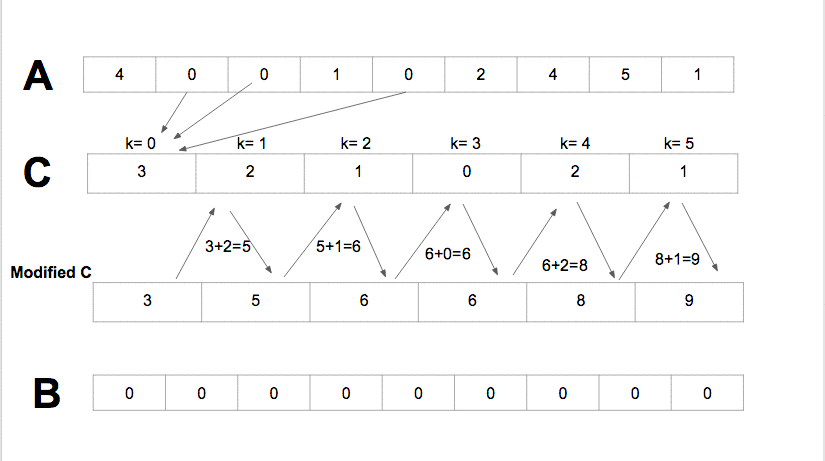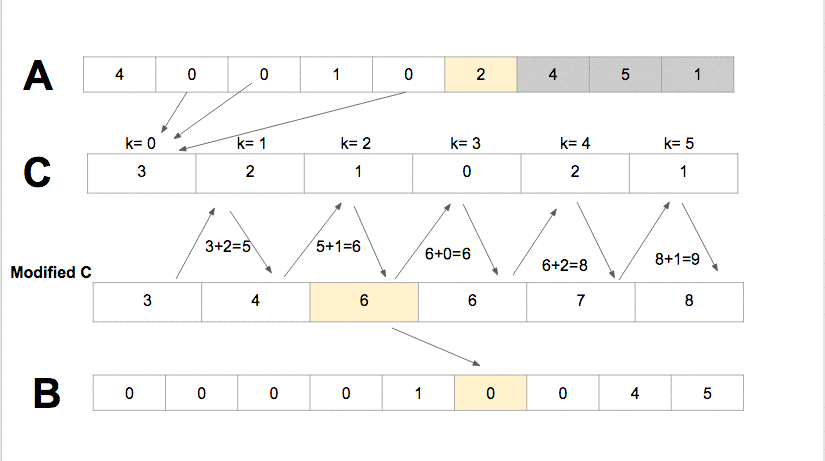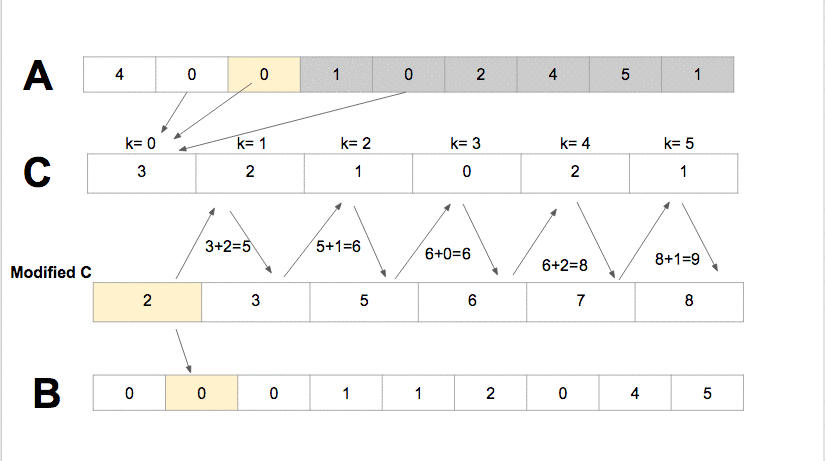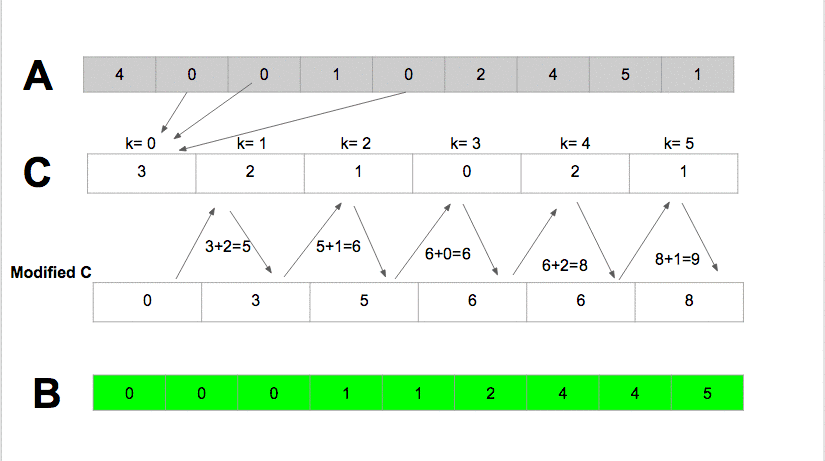
Source code minh hoạ

def counting_sort(A, digit, radix):
    #"A" is a list to be sorted, radix is the base of the number system, digit is the digit
    #we want to sort by

    #create a list B which will be the sorted list
    B = [0]*len(A)
    C = [0]*int(radix)
    #counts the number of occurences of each digit in A 
    for i in range(0, len(A)):
        digit_of_Ai = (A[i]/radix**digit)%radix
        C[digit_of_Ai] = C[digit_of_Ai] +1 
        #now C[i] is the value of the number of elements in A equal to i

    #this FOR loop changes C to show the cumulative # of digits up to that index of C
    for j in range(1,radix):
        C[j] = C[j] + C[j-1]
        #here C is modifed to have the number of elements <= i
    for m in range(len(A)-1, -1, -1): #to count down (go through A backwards)
        digit_of_Ai = (A[m]/radix**digit)%radix
        C[digit_of_Ai] = C[digit_of_Ai] -1
        B[C[digit_of_Ai]] = A[m]

    return B

#alist = [9,3,1,4,5,7,7,2,2]
#print counting_sort(alist,0,10)

Độ phức tạp thuật toán

Time complexity : O(n+k).
Space complexity: O(k) - k là max key value.

Ưu điểm

Khi độ dài của array/list đầu vào không nhỏ hơn key lớn nhất k, thì độ phức tạp thuật toán sẽ là O(n), trong khi với các thuật toán khác sẽ là O(nlogn).

Nhược điểm

Counting sort sử dụng key - value như là index trong một mảng, nên nó không phải là comparison sort, và không phù hợp với những array/list có key value lớn.

Ứng dụng

Counting sort có thể được sử dụng để giải quyết 1 phần trong các thuật toán sắp xếp khác mà có thể sắp xếp với key value lớn hơn như radixsort.

3.2 Bucket sort

Tên gọi khác bin sort, là comparison sort, và là thuật toán sắp xếp bằng cách phân phối các phần tử trong array ban đầu vào các bucket tương ứng.

Ý tưởng

đầu tiên tạo ra 1 array chứa các buckets rỗng.
Scatter: duyệt array ban đầu và cho các phần tử vào các bucket tương ứng.
Sắp xếp từng phần bucket không rỗng
Gather: duyệt qua các bucket theo thứ tự, và đẩy các phần tử vào mảng ban đầu.

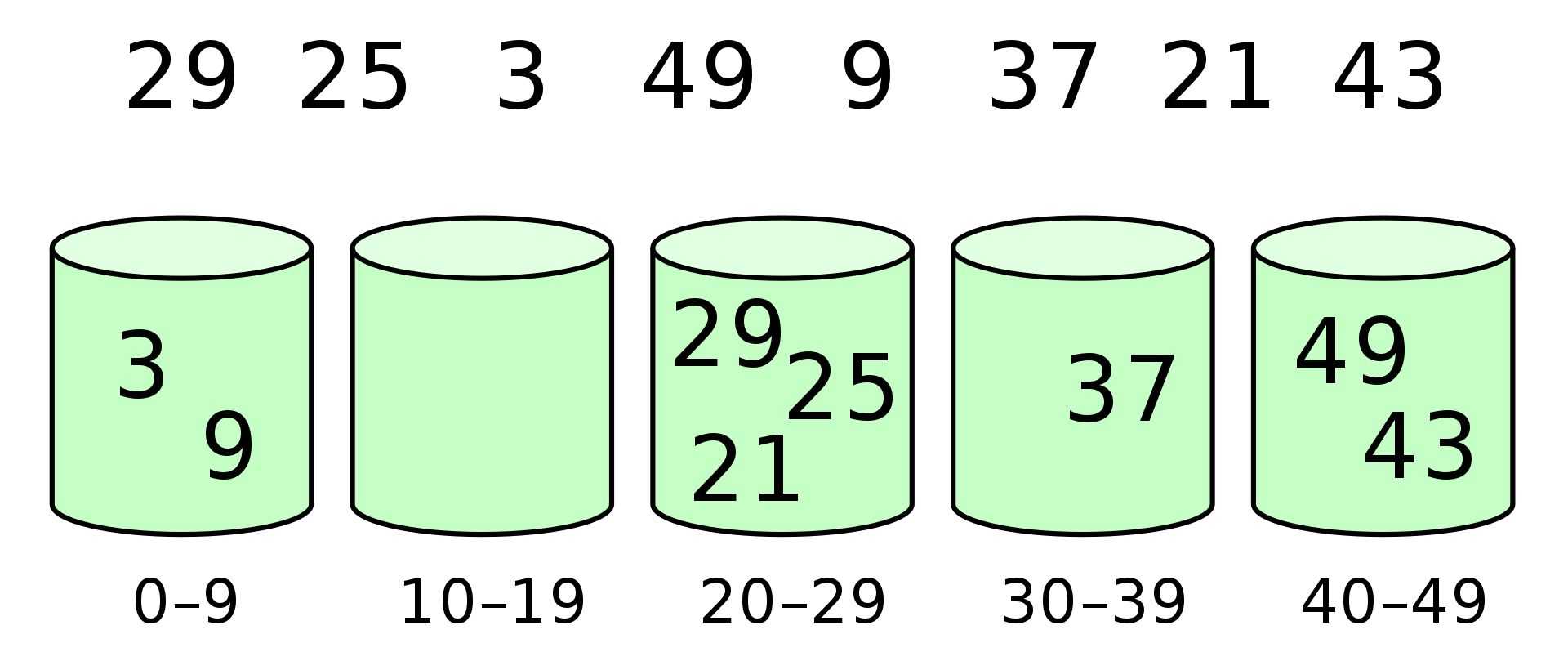
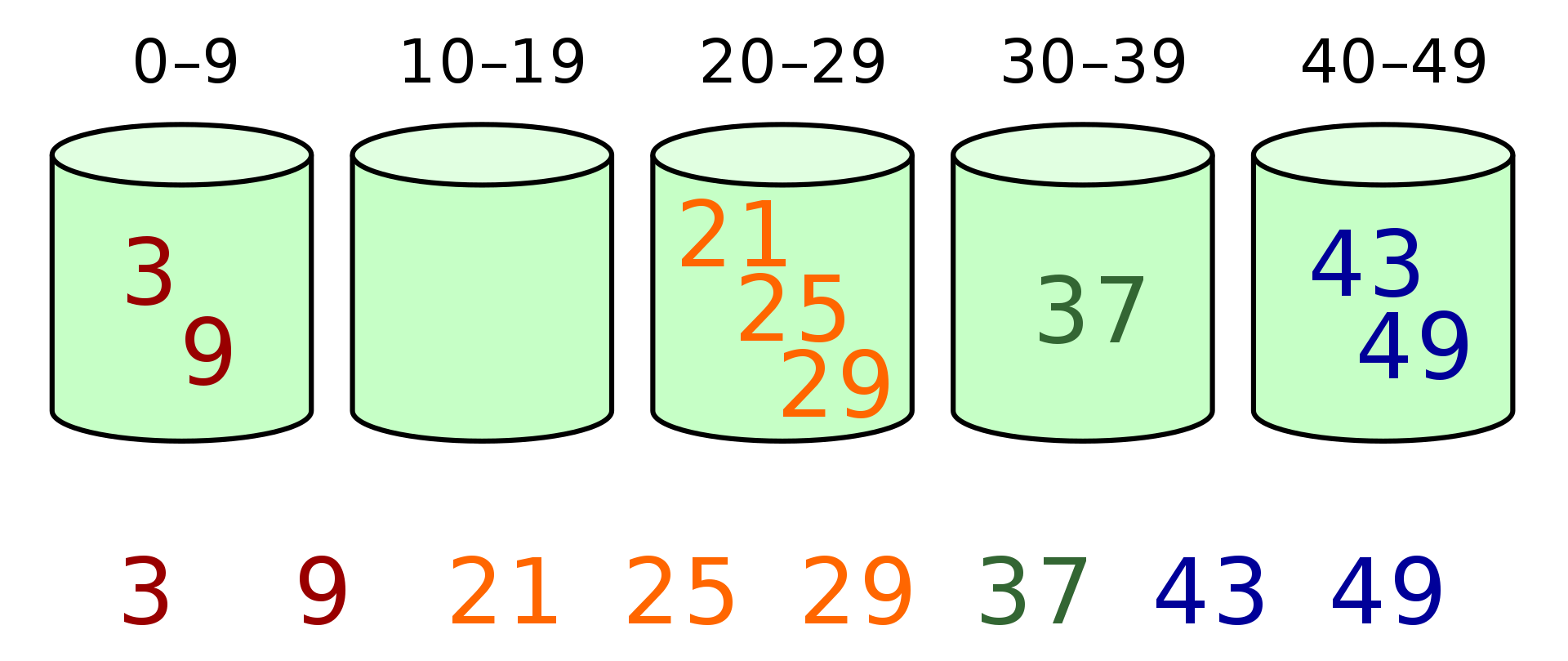
Source code minh hoạ

# Python3 program to sort an array  
# using bucket sort  
def insertionSort(b): 
    for i in range(1, len(b)): 
        up = b[i] 
        j = i - 1
        while j >= 0 and b[j] > up:  
            b[j + 1] = b[j] 
            j -= 1
        b[j + 1] = up      
    return b      
              
def bucketSort(x): 
    arr = [] 
    slot_num = 10 # 10 means 10 slots, each 
                  # slot's size is 0.1 
    for i in range(slot_num): 
        arr.append([]) 
          
    # Put array elements in different buckets  
    for j in x: 
        index_b = int(slot_num * j)  
        arr[index_b].append(j) 
      
    # Sort individual buckets  
    for i in range(slot_num): 
        arr[i] = insertionSort(arr[i]) 
          
    # concatenate the result 
    k = 0
    for i in range(slot_num): 
        for j in range(len(arr[i])): 
            x[k] = arr[i][j] 
            k += 1
    return x 

Độ phức tạp thuật toán

Time complexity: average O(n+k), worst case O(n^2)
Space complexity O(n)

Ưu điểm

Ổn định.

Nhược điểm

Độ phức tạp thuật toán phụ thuộc vào việc sắp xếp từng bucket, số lượng bucket, và việc input đã được phân phối đồng nhất hay chưa (continuous uniform distribution).

Ứng dụng

Bucket sort có thể coi là tổng quát hoá của counting sort. (Khi mỗi bucket có size là 1, thì bucket sort chính là counting sort).
Bucket sort với 2 bucket là một phiên bản tối ưu của quicksort khi mà pivot value luôn luôn được chọn là middle value của tập value đang xét.
Radix sort mà cài đặt theo top-down được xem như trường hợp đặc biệt của bucket sort với size của mỗi bucket là cơ số mũ của 2.

3.3 Radix sort

Là thuật toán sắp xếp không dựa trên sự so sánh giữa hai phần tử, mà bằng cách tạo và phân phối các phần tử trong mảng ban đầu vào các bucket theo cơ số (radix) của nó.

Ý tưởng

Đầu tiên, thuật toán sẽ chia các phần tử thành các nhóm, dựa trên chữ số cuối cùng (hoặc dựa theo bit cuối cùng, hoặc vài bit cuối cùng).
Sau đó ta đưa các nhóm lại với nhau, và được danh sách sắp xếp theo chữ số cuối của các phần tử. Quá trình này lặp đi lặp lại với chữ số át cuối cho tới khi tất cả vị trí chữ số đã sắp xếp.

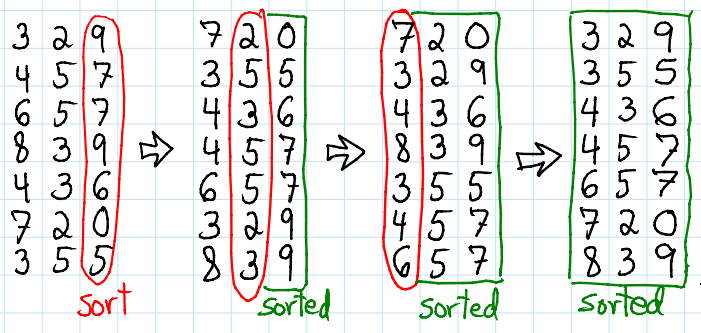
Source code minh hoạ

def counting_sort(A, digit, radix):
    #"A" is a list to be sorted, radix is the base of the number system, digit is the digit
    #we want to sort by

    #create a list B which will be the sorted list
    B = [0]*len(A)
    C = [0]*int(radix)
    #counts the number of occurences of each digit in A 
    for i in range(0, len(A)):
        digit_of_Ai = (A[i]/radix**digit)%radix
        C[digit_of_Ai] = C[digit_of_Ai] +1 
        #now C[i] is the value of the number of elements in A equal to i

    #this FOR loop changes C to show the cumulative # of digits up to that index of C
    for j in range(1,radix):
        C[j] = C[j] + C[j-1]
        #here C is modifed to have the number of elements <= i
    for m in range(len(A)-1, -1, -1): #to count down (go through A backwards)
        digit_of_Ai = (A[m]/radix**digit)%radix
        C[digit_of_Ai] = C[digit_of_Ai] -1
        B[C[digit_of_Ai]] = A[m]

    return B

#alist = [9,3,1,4,5,7,7,2,2]
#print countingSort(alist,0,10)

def radix_sort(A, radix):
    #radix is the base of the number system
    #k is the largest number in the list
    k = max(A)
    #output is the result list we will build
    output = A
    #compute the number of digits needed to represent k
    digits = int(math.floor(math.log(k, radix)+1))
    for i in range(digits):
        output = counting_sort(output,i,radix)

    return output

Độ phức tạp thuật toán

Time complexity: O(nk), k - max độ dài của key value.
Space complexity: O(n+k)

Ưu điểm

Ổn định.
Có thể chạy nhanh hơn các thuật toán sắp xếp sử dụng so sánh. Ví dụ nếu ta sắp xếp các số nguyên 32 bit, và chia nhóm theo 1 bit, thì độ phức tạp là O(n).

Nhược điểm

Không thể sắp xếp số thực.

Ứng dụng

Radix sort có thể áp dụng cho các dữ liệu mà có thể sắp xếp theo thứ tự từ điển, chúng có thể là integer, word, card, hay mail.
Radix sorts là thuật toán sắp xếp tối ưu được sử dụng trên parallel machines.

0. Sort Algorithms Overview - Theo VNOI

1. Simple sorts

1.1 Bubble sort - Theo VNOI

1.2 Insertion sort

1.3 Selection sort

2. Efficient sorts

2.1 Mergesort

2.2 Heapsort

2.3 Quicksort - Theo VNOI

3. Distribution sort

3.1 Counting sort

3.2 Bucket sort

3.3 Radix sort

Tài liệu tham khảo